The Global Liquidity Cycle
Where Are We Now?
Origins
This report looks at the origins, definitions and outlook for Global Liquidity. It is part primer and part prediction.
The earliest things you learn often stay with you. Our key insight came from the bond markets and specifically how the US Treasury yield curve reacts to the cycle of funding liquidity. We learned this decades ago at Salomon Brothers and it stuck: more liquidity induces a steeper yield curve, less liquidity means a flattening curve. The latest steepening the US Treasury yield curve confirms that US liquidity has been improving for some months. Evidence the chart below, where our index of US Liquidity has been advanced by 9 months to show that it is predictive. It filled the coffers of Salomon’s traders, but for years we puzzled over why this linkage should exist?
The US Liquidity Cycle (Advanced 9 months) and the US Treasury 10-2 Year Yield Curve, 2005-23
The best explanation relies on term premia, the compensation paid to investors for holding interest rate risk. Term premia are a main factor driving the slope of the curve. The efficient market hypothesis tells us that term premia should be negligible over the long-term. However, they fluctuate over most investment horizons. Since year 2000, some 80% of the variation in 10-year Treasury yields can be related to term premia movements, according to the ACM bond data provided by the New York Fed.
One reason term premia vary is because they reflect the excess demand and supply for Treasuries. In periods when there is excess supply of Treasuries, term premia are typically high and positive. In periods of excess demand, they tend to be low or negative. Treasuries are often held by banks, insurance funds and major investors because they are deemed to be ‘safe’ assets by many regulators. In other words, they are liquid and their prices should be largely predictable.
Why are term premia linked to Liquidity? During periods of tight liquidity, when systemic risks are high and defaults more frequent, the demand for ‘safe’ asset increases and term premia tend to fall. Equivalently, during periods of abundant liquidity the reverse occurs, and investors switch out of ‘safe’ assets into more risky investments, such as equities and corporate bonds. Hence, rising liquidity is associated with increasing term premia. Because term premia have greatest impact at longer duration bond tenors, this explains why the yield curve steepens (e.g. the term premium on a 3-month bill is negligible).
Admittedly, this description runs counter to the traditional QE (quantitative easing) narrative which argues that Central Bank bond purchases push down yields by bidding up prices and so reducing term premia. This argument relies on an increasing scarcity of Treasuries available for the private sector. It is hard to argue against this as a fact in the short-term. However, beyond a window of days or weeks, the evidence runs much the other way. This is because what is ignored is the second-round impact of rising Central Bank liquidity injections (the corollary of QE purchases) on the private sector’s demand for ‘safe’ assets. More system-wide liquidity reduces the attractions of ‘safe’ assets. In short, the demand curve for ‘safe’ assets shifts leftwards causing Treasury bond prices to fall and yields and term premia to rise.
How We Measure Liquidity
Liquidity is plainly important. We monitor Global Liquidity, because for the most part (outside of crises) national sources of liquidity are fungible, i.e. they flow. We cover close to 80 economies. Global Liquidity is a US$170 trillion dollar funding pool that we measure through taking sources of funds from the assets-side of the private sector balance sheet. It comprises the short-term liabilities of credit providers, such as banks and shadow banks. It also includes the cash flows households and corporations. Because we are interested in flows through asset markets, this funding-based definition of ‘liquidity’ focuses on the financial sector. As such, it largely begins where traditional money supply measures like M1 end.
The cash flow equation reported in the slide above shows the maths behind our definition. In contrast to most economic statistics, which are net flows, ‘liquidity’ is a gross balance sheet concept that measures the capacity of capital. The equation shows that sources of funds, i.e. ‘liquidity’, namely savings (S) and changes in financial liabilities (ΔFL) must, by definition, equal uses of funds, such as new capital investment (I) and changes in the value of asset holdings (ΔFA).
It follows that the overall private sector balance sheet can expand (i.e both FA and FL increase) but net savings (S-I) remain unchanged. In this case, ‘liquidity’ expands independently of savings.
Sources of funds (S+ ΔFL) typically drive uses of funds (I+ΔFA), but it is also true that rising collateral values (ΔFA) subsequently encourage second-round effects that further expand lending and so boost liquidity.
This elasticity in the liquidity-creation mechanism is crucial. It bests the conventional explanations of excess liquidity, such as the widely-quoted ‘savings glut’ view. This became the popular explanation of the 2008/09 GFC and is associated with former Federal Reserve Chair Ben Bernanke. Bernanke argued that abundant Asian savings flows inflated the US asset bubble. This seems unlikely in terms of scale. However, Asian savings flows (S) may have initially triggered an increase in liquidity that subsequently became amplified by rapacious banks and shadow banks (ΔFL −› ΔFA −› ΔFL) into a huge tsunami of liquidity.
In this transmission, the elasticity of the liquidity mechanism becomes dominant. Some have more correctly dubbed this a ‘banking glut’ rather than a ‘savings glut’.
Timing The Liquidity Cycle
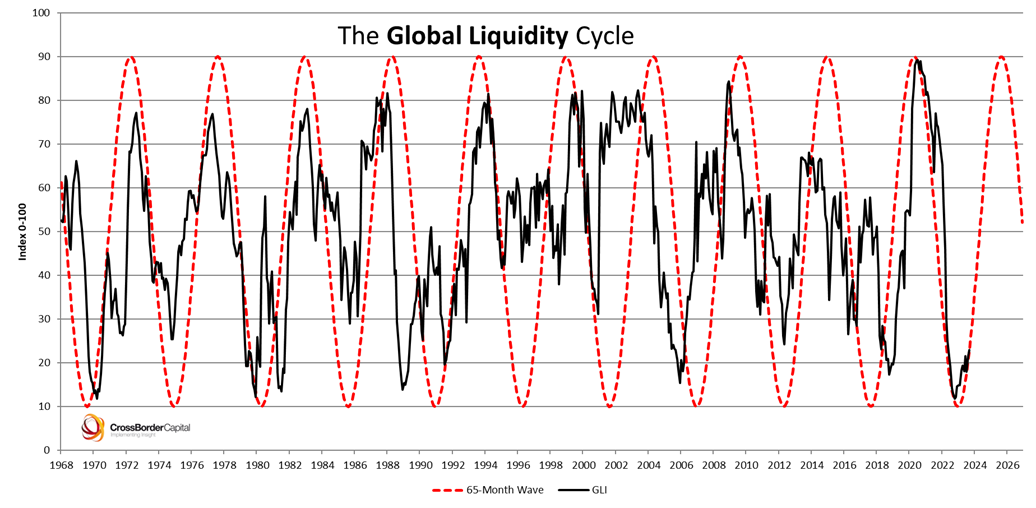
The cycle of Global Liquidity is shown in the following chart. Global Liquidity is measured here as a normalised index (GLI), which essentially captures its momentum. We use it to facilitate comparisons over-time and between countries. The index is designed to have a 0-100 range, with a mean set at 50.
The data reported in the chart have been plotted alongside a repeating cycle, or sine wave, of average duration 65 months (i.e. between 5-6 years). This frequency was originally estimated over the 1965-2000 period using Fourier analysis. It has been extrapolated thereafter.
The coincidence of the two cycles (the GLI and the sine wave) not only confirms (or not) the accuracy of our estimate of the cycle length, it also allows us to project the cycle forwards in time to predict the next peaks and troughs.
According to the extrapolated data, the Global Liquidity Cycle should next peak around September 2025, following its December 2022 trough.
